GitHubSeob
C++ / 백준 / 2610 / 회의준비 본문
| 문제 |
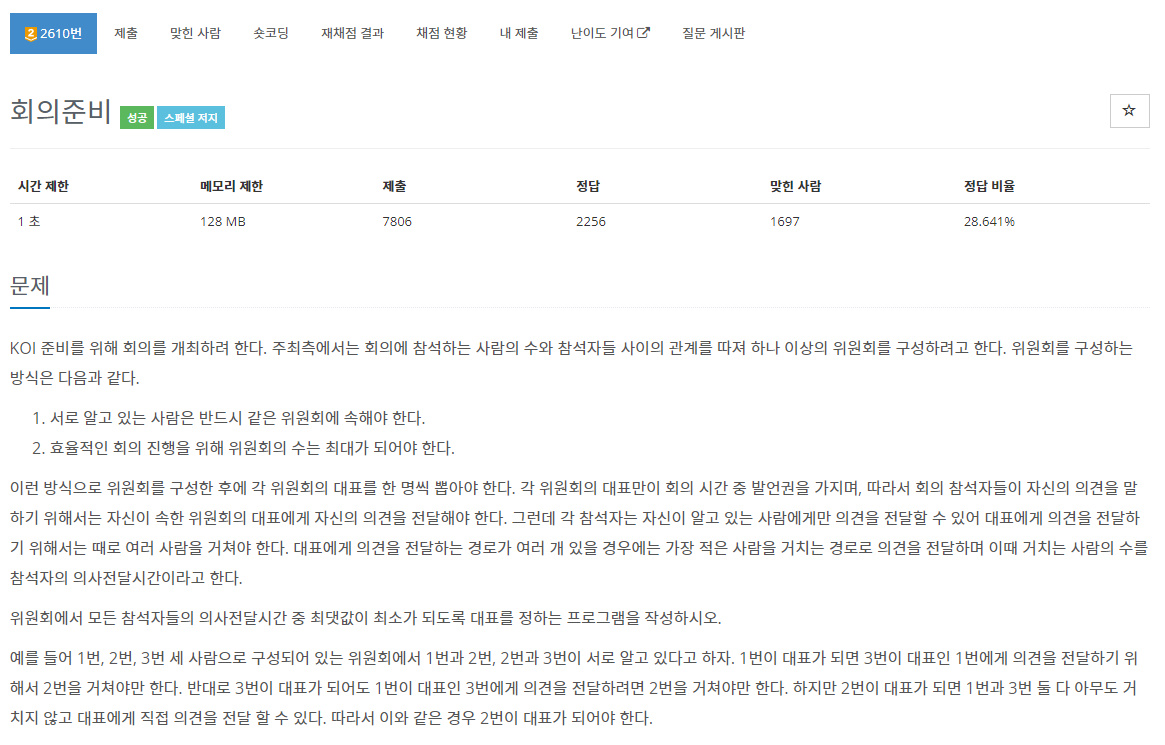
https://www.acmicpc.net/problem/2610
2610번: 회의준비
첫째 줄에 회의에 참석하는 사람의 수 N이 주어진다. 참석자들은 1부터 N까지의 자연수로 표현되며 회의에 참석하는 인원은 100 이하이다. 둘째 줄에는 서로 알고 있는 관계의 수 M이 주어진다. 이
www.acmicpc.net

| 문제풀이 |
플로이드 와샬 알고리즘으로 문제를 풀었다.
먼저 1부터 사용하기 때문에 N+1 * N+1 크기의 2차원 벡터를 만들고 -1로 초기화한다.
플로이드 와샬 알고리즘을 이용하여 2차원 벡터에 P1가 몇 번 만에 P2를 만날 수 있는지를 저장한다.
그다음 그룹으로 묶고 그룹에서 거쳐가는 횟수의 최댓값이 가장 작은 사람을 구한다.
for (mid = 1; mid <= N; ++mid) {
for (P1 = 1; P1 <= N; ++P1) {
for (P2 = 1; P2 <= N; ++P2) {
if (cmte[P1][mid] == X || cmte[mid][P2] == X) {
continue;
}
if (cmte[P1][P2] == X) {
cmte[P1][P2] = cmte[P1][mid] + cmte[mid][P2];
}
else {
cmte[P1][P2] = min(cmte[P1][P2], cmte[P1][mid] + cmte[mid][P2]);
}
}
}
}보통 2차원 벡터를 초기화할 때는 MAX값으로 두고 값을 입력받고 min값을 구하지만, 벡터의 최댓값을 구하는 max_element함수를 이용할 것이므로 -1로 초기화했다.
삼중 반복문에서 반복을 하는 과정에서 [P1][P2]를 구하고 싶을 때 [P1][mid] or [mid][P2]가 -1이면 만날 수 없으므로 넘어간다. -1이 껴 있으므로 min을 구할 때 조심해야 한다.
for (P1 = 1; P1 <= N; ++P1) {
if (visited[P1] == false) {
max_cnt = 10001;
for (P2 = P1; P2 <= N; ++P2) {
if (cmte[P1][P2] != X && visited[P2] == false) {
visited[P2] = true;
cnt = *max_element(cmte[P2].begin(), cmte[P2].end());
if (max_cnt > cnt) {
rep = P2;
max_cnt = cnt;
}
}
}
answer.push_back(rep);
}
}삼중 반복문이 끝나 P1에서 P2로 가는 횟수를 모두 알아냈으면 그룹으로 나눠야 한다.
bool형태의 visited벡터를 이용해 그룹원들을 구할 것이다.
여기서 그룹원들은 서로서로 사람을 통해 만날 수 있는 사람들의 모임이다.
P1은 1부터 N까지 탐색한다.
P2는 P1부터 N까지 탐색한다.
방문한 적이 없는 사람이면 P1이 속해있는 그룹으로 묶을 것이다.
그룹으로 묶으면서 cmte[P2]의 모든 값들을 탐색하면서 가장 큰 값을 cnt에 저장한다.
(여기서 max_element를 통해 반복문을 사용하지 않고 간단하게 구할 것이므로 초반에 벡터를 -1로 초기화했다.
10001로 초기화했더니 max_element에 10001만 저장이 됐었다..)
그다음 max_cnt와 비교해서 cnt가 더 적다면 P2가 대표로 된다.
P2가 N이 됐다면 P1과 연결된 사람은 모두 탐색이 된 것이므로 P1과 연결된 그룹 중 대표를 answer벡터에 저장한다.
주의할 점은 거치는 사람의 횟수의 합의 최솟값인 사람을 구하는 것이 아닌, 거치는 사람의 횟수의 MAX가 최소가 되는 사람을 구하는 것이다.
cmte[1][2]=10, cmte[1][3]=12로 가정하자, 여기서 1번 사람은 2와 3을 만나려면 총 22번을 거쳐야 한다.
그러나 이 문제에서 구하는 것은 '의사전달시간 중 최댓값이 최소가 되도록 하는 대표'를 구하는 것이다.
따라서 이 부분에서 필요한 것은 cmte[1][3]=12 이 부분이다. 그래서 합이 아닌 max_element를 이용해 구한 것이다.
| 코드 |
#include <iostream>
#include <vector>
#include <algorithm>
#define X -1
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
int N(0), M(0), idx(0), P1(0), P2(0), mid(0);
int rep(0), cnt(0), max_cnt(0);
cin >> N >> M;
vector<vector<int>>cmte(N + 1, vector<int>(N + 1, X));
vector<bool>visited(N + 1, false);
vector<int>answer;
for (idx = 0; idx < M; ++idx) {
cin >> P1 >> P2;
cmte[P1][P2] = 1;
cmte[P2][P1] = 1;
}
for (idx = 1; idx <= N; ++idx) {
cmte[idx][idx] = 0;
}
for (mid = 1; mid <= N; ++mid) {
for (P1 = 1; P1 <= N; ++P1) {
for (P2 = 1; P2 <= N; ++P2) {
if (cmte[P1][mid] == X || cmte[mid][P2] == X) {
continue;
}
if (cmte[P1][P2] == X) {
cmte[P1][P2] = cmte[P1][mid] + cmte[mid][P2];
}
else {
cmte[P1][P2] = min(cmte[P1][P2], cmte[P1][mid] + cmte[mid][P2]);
}
}
}
}
for (P1 = 1; P1 <= N; ++P1) {
if (visited[P1] == false) {
max_cnt = 10001;
for (P2 = P1; P2 <= N; ++P2) {
if (cmte[P1][P2] != X && visited[P2] == false) {
visited[P2] = true;
cnt = *max_element(cmte[P2].begin(), cmte[P2].end());
if (max_cnt > cnt) {
rep = P2;
max_cnt = cnt;
}
}
}
answer.push_back(rep);
}
}
sort(answer.begin(), answer.end());
cout << answer.size() << '\n';
for (idx = 0; idx < answer.size(); ++idx) {
cout << answer[idx] << '\n';
}
}
'Baekjoon > Gold' 카테고리의 다른 글
| C++ / 백준 / 21758 / 꿀 따기 (0) | 2023.07.04 |
|---|---|
| C++ / 백준 / 10282 / 해킹 (0) | 2023.07.03 |
| C++ / 백준 / 1613 / 역사 (0) | 2023.07.03 |
| C++ / 백준 / 11404 / 플로이드 (0) | 2023.07.02 |
| C++ / 백준 / 1238 / 파티 (0) | 2023.07.01 |




